这次的逆向蛮简单的,比之前的几场简单多了,感觉就是签到难度。逆向第三题是智能合约,没接触过,不会做。
re-z3
第一题标题是z3,所以是想让我们用z3解,不过我个人更喜欢matlab。
刚开始没解出来是因为正则表达式提取方程式系数出了点小意外,很快就修改了。提取脚本如下。代码看着有点长,其实大多是可以复制粘贴的。
import struct
#with open(r'd:\dump', 'rb')as f:
# b = f.read()
#print(b)
b = b'\x17O\x00\x00\xf6\x9c\x00\x00\xdb\x8d\x00\x00\xa6\x8e\x00\x00)i\x00\x00\x11\x99\x00\x00\xa2@\x00\x00>/\x00\x00\xb6b\x00\x00\x82K\x00\x00lH\x00\x00\x02@\x00\x00\xd7R\x00\x00\xef-\x00\x00\xdc(\x00\x00\rd\x00\x00\x8fR\x00\x00;a\x00\x00\x81G\x00\x00\x17k\x00\x0072\x00\x00\x93*\x00\x00_a\x00\x00\xbeP\x00\x00\x8eY\x00\x00VF\x00\x001[\x00\x00:1\x00\x00\x100\x00\x00\xfeg\x00\x00_M\x00\x00\xdbX\x00\x00\x997\x00\x00\xa0`\x00\x00P\'\x00\x00Y7\x00\x00S\x89\x00\x00"q\x00\x00\xf9\x81\x00\x00$U\x00\x00q\x89\x00\x00\x1d:\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'
c = []
for i in range(42):
a = b[i*4:i*4+4]
n = struct.unpack('I', a)
c.append(n[0])
print(n[0],end=';')
print()
print(len(c))
s = '''v4 = 34 * v49 + 12 * v46 + 53 * v47 + 6 * v48 + 58 * v50 + 36 * v51 + v52;
v5 = 27 * v50 + 73 * v49 + 12 * v48 + 83 * v46 + 85 * v47 + 96 * v51 + 52 * v52;
v6 = 24 * v48 + 78 * v46 + 53 * v47 + 36 * v49 + 86 * v50 + 25 * v51 + 46 * v52;
v7 = 78 * v47 + 39 * v46 + 52 * v48 + 9 * v49 + 62 * v50 + 37 * v51 + 84 * v52;
v8 = 48 * v50 + 14 * v48 + 23 * v46 + 6 * v47 + 74 * v49 + 12 * v51 + 83 * v52;
v9 = 15 * v51 + 48 * v50 + 92 * v48 + 85 * v47 + 27 * v46 + 42 * v49 + 72 * v52;
v10 = 26 * v51 + 67 * v49 + 6 * v47 + 4 * v46 + 3 * v48 + 68 * v52;
v11 = 34 * v56 + 12 * v53 + 53 * v54 + 6 * v55 + 58 * v57 + 36 * v58 + v59;
v12 = 27 * v57 + 73 * v56 + 12 * v55 + 83 * v53 + 85 * v54 + 96 * v58 + 52 * v59;
v13 = 24 * v55 + 78 * v53 + 53 * v54 + 36 * v56 + 86 * v57 + 25 * v58 + 46 * v59;
v14 = 78 * v54 + 39 * v53 + 52 * v55 + 9 * v56 + 62 * v57 + 37 * v58 + 84 * v59;
v15 = 48 * v57 + 14 * v55 + 23 * v53 + 6 * v54 + 74 * v56 + 12 * v58 + 83 * v59;
v16 = 15 * v58 + 48 * v57 + 92 * v55 + 85 * v54 + 27 * v53 + 42 * v56 + 72 * v59;
v17 = 26 * v58 + 67 * v56 + 6 * v54 + 4 * v53 + 3 * v55 + 68 * v59;
v18 = 34 * v63 + 12 * v60 + 53 * v61 + 6 * v62 + 58 * v64 + 36 * v65 + v66;
v19 = 27 * v64 + 73 * v63 + 12 * v62 + 83 * v60 + 85 * v61 + 96 * v65 + 52 * v66;
v20 = 24 * v62 + 78 * v60 + 53 * v61 + 36 * v63 + 86 * v64 + 25 * v65 + 46 * v66;
v21 = 78 * v61 + 39 * v60 + 52 * v62 + 9 * v63 + 62 * v64 + 37 * v65 + 84 * v66;
v22 = 48 * v64 + 14 * v62 + 23 * v60 + 6 * v61 + 74 * v63 + 12 * v65 + 83 * v66;
v23 = 15 * v65 + 48 * v64 + 92 * v62 + 85 * v61 + 27 * v60 + 42 * v63 + 72 * v66;
v24 = 26 * v65 + 67 * v63 + 6 * v61 + 4 * v60 + 3 * v62 + 68 * v66;
v25 = 34 * v70 + 12 * v67 + 53 * v68 + 6 * v69 + 58 * v71 + 36 * v72 + v73;
v26 = 27 * v71 + 73 * v70 + 12 * v69 + 83 * v67 + 85 * v68 + 96 * v72 + 52 * v73;
v27 = 24 * v69 + 78 * v67 + 53 * v68 + 36 * v70 + 86 * v71 + 25 * v72 + 46 * v73;
v28 = 78 * v68 + 39 * v67 + 52 * v69 + 9 * v70 + 62 * v71 + 37 * v72 + 84 * v73;
v29 = 48 * v71 + 14 * v69 + 23 * v67 + 6 * v68 + 74 * v70 + 12 * v72 + 83 * v73;
v30 = 15 * v72 + 48 * v71 + 92 * v69 + 85 * v68 + 27 * v67 + 42 * v70 + 72 * v73;
v31 = 26 * v72 + 67 * v70 + 6 * v68 + 4 * v67 + 3 * v69 + 68 * v73;
v32 = 34 * v77 + 12 * v74 + 53 * v75 + 6 * v76 + 58 * v78 + 36 * v79 + v80;
v33 = 27 * v78 + 73 * v77 + 12 * v76 + 83 * v74 + 85 * v75 + 96 * v79 + 52 * v80;
v34 = 24 * v76 + 78 * v74 + 53 * v75 + 36 * v77 + 86 * v78 + 25 * v79 + 46 * v80;
v35 = 78 * v75 + 39 * v74 + 52 * v76 + 9 * v77 + 62 * v78 + 37 * v79 + 84 * v80;
v36 = 48 * v78 + 14 * v76 + 23 * v74 + 6 * v75 + 74 * v77 + 12 * v79 + 83 * v80;
v37 = 15 * v79 + 48 * v78 + 92 * v76 + 85 * v75 + 27 * v74 + 42 * v77 + 72 * v80;
v38 = 26 * v79 + 67 * v77 + 6 * v75 + 4 * v74 + 3 * v76 + 68 * v80;
v39 = 34 * v84 + 12 * v81 + 53 * v82 + 6 * v83 + 58 * v85 + 36 * v86 + v87;
v40 = 27 * v85 + 73 * v84 + 12 * v83 + 83 * v81 + 85 * v82 + 96 * v86 + 52 * v87;
v41 = 24 * v83 + 78 * v81 + 53 * v82 + 36 * v84 + 86 * v85 + 25 * v86 + 46 * v87;
v42 = 78 * v82 + 39 * v81 + 52 * v83 + 9 * v84 + 62 * v85 + 37 * v86 + 84 * v87;
v43 = 48 * v85 + 14 * v83 + 23 * v81 + 6 * v82 + 74 * v84 + 12 * v86 + 83 * v87;
v44 = 15 * v86 + 48 * v85 + 92 * v83 + 85 * v82 + 27 * v81 + 42 * v84 + 72 * v87;
v45 = 26 * v86 + 67 * v84 + 6 * v82 + 4 * v81 + 3 * v83 + 68 * v87;'''
import re
lines = s.split('\n')
for line in lines:
# print(line)
left = [0] * 42
r = re.search(r'v(\d+?) = (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?);', line)
if r:
left[int(r.group(3)) - 46] = int(r.group(2))
left[int(r.group(5)) - 46] = int(r.group(4))
left[int(r.group(7)) - 46] = int(r.group(6))
left[int(r.group(9)) - 46] = int(r.group(8))
left[int(r.group(11)) - 46] = int(r.group(10))
left[int(r.group(13)) - 46] = int(r.group(12))
else:
r = re.search(r'v(\d+?) = (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?);', line)
if r:
left[int(r.group(3)) - 46] = int(r.group(2))
left[int(r.group(5)) - 46] = int(r.group(4))
left[int(r.group(7)) - 46] = int(r.group(6))
left[int(r.group(9)) - 46] = int(r.group(8))
left[int(r.group(11)) - 46] = int(r.group(10))
left[int(r.group(13)) - 46] = int(r.group(12))
left[int(r.group(15)) - 46] = int(r.group(14))
else:
r = re.search(r'v(\d+?) = (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ (\d+?) \* v(\d+?) \+ v(\d+?);', line)
left[int(r.group(3)) - 46] = int(r.group(2))
left[int(r.group(5)) - 46] = int(r.group(4))
left[int(r.group(7)) - 46] = int(r.group(6))
left[int(r.group(9)) - 46] = int(r.group(8))
left[int(r.group(11)) - 46] = int(r.group(10))
left[int(r.group(13)) - 46] = int(r.group(12))
left[int(r.group(14)) - 46] = 1
for i in range(42):
if i != 41:
print(left[i], end=',')
else:
print(left[i], end=';\n')然后是索然无味的matlab:
>> A = [12,53,6,34,58,36,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
83,85,12,73,27,96,52,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
78,53,24,36,86,25,46,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
39,78,52,9,62,37,84,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
23,6,14,74,48,12,83,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
27,85,92,42,48,15,72,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
4,6,3,67,0,26,68,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,12,53,6,34,58,36,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,83,85,12,73,27,96,52,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,78,53,24,36,86,25,46,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,39,78,52,9,62,37,84,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,23,6,14,74,48,12,83,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,27,85,92,42,48,15,72,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,4,6,3,67,0,26,68,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,12,53,6,34,58,36,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,83,85,12,73,27,96,52,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,78,53,24,36,86,25,46,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,39,78,52,9,62,37,84,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,23,6,14,74,48,12,83,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,27,85,92,42,48,15,72,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,4,6,3,67,0,26,68,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,12,53,6,34,58,36,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,83,85,12,73,27,96,52,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,78,53,24,36,86,25,46,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,39,78,52,9,62,37,84,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,23,6,14,74,48,12,83,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,27,85,92,42,48,15,72,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,4,6,3,67,0,26,68,0,0,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,12,53,6,34,58,36,1,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,83,85,12,73,27,96,52,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,78,53,24,36,86,25,46,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,39,78,52,9,62,37,84,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,23,6,14,74,48,12,83,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,27,85,92,42,48,15,72,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,4,6,3,67,0,26,68,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,12,53,6,34,58,36,1;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,83,85,12,73,27,96,52;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,78,53,24,36,86,25,46;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,39,78,52,9,62,37,84;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,23,6,14,74,48,12,83;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,27,85,92,42,48,15,72;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,4,6,3,67,0,26,68]
A =
Columns 1 through 24
12 53 6 34 58 36 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
83 85 12 73 27 96 52 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
78 53 24 36 86 25 46 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
39 78 52 9 62 37 84 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
23 6 14 74 48 12 83 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
27 85 92 42 48 15 72 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4 6 3 67 0 26 68 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 12 53 6 34 58 36 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 83 85 12 73 27 96 52 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 78 53 24 36 86 25 46 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 39 78 52 9 62 37 84 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 23 6 14 74 48 12 83 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 27 85 92 42 48 15 72 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 4 6 3 67 0 26 68 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 53 6 34 58 36 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 83 85 12 73 27 96 52 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 78 53 24 36 86 25 46 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 39 78 52 9 62 37 84 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 23 6 14 74 48 12 83 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 27 85 92 42 48 15 72 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 6 3 67 0 26 68 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 53 6
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 83 85 12
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 78 53 24
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 39 78 52
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 23 6 14
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 27 85 92
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 6 3
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Columns 25 through 42
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
34 58 36 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
73 27 96 52 0 0 0 0 0 0 0 0 0 0 0 0 0 0
36 86 25 46 0 0 0 0 0 0 0 0 0 0 0 0 0 0
9 62 37 84 0 0 0 0 0 0 0 0 0 0 0 0 0 0
74 48 12 83 0 0 0 0 0 0 0 0 0 0 0 0 0 0
42 48 15 72 0 0 0 0 0 0 0 0 0 0 0 0 0 0
67 0 26 68 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 12 53 6 34 58 36 1 0 0 0 0 0 0 0
0 0 0 0 83 85 12 73 27 96 52 0 0 0 0 0 0 0
0 0 0 0 78 53 24 36 86 25 46 0 0 0 0 0 0 0
0 0 0 0 39 78 52 9 62 37 84 0 0 0 0 0 0 0
0 0 0 0 23 6 14 74 48 12 83 0 0 0 0 0 0 0
0 0 0 0 27 85 92 42 48 15 72 0 0 0 0 0 0 0
0 0 0 0 4 6 3 67 0 26 68 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 12 53 6 34 58 36 1
0 0 0 0 0 0 0 0 0 0 0 83 85 12 73 27 96 52
0 0 0 0 0 0 0 0 0 0 0 78 53 24 36 86 25 46
0 0 0 0 0 0 0 0 0 0 0 39 78 52 9 62 37 84
0 0 0 0 0 0 0 0 0 0 0 23 6 14 74 48 12 83
0 0 0 0 0 0 0 0 0 0 0 27 85 92 42 48 15 72
0 0 0 0 0 0 0 0 0 0 0 4 6 3 67 0 26 68
>> B = [20247;40182;36315;36518;26921;39185;16546;12094;25270;19330;18540;16386;21207;11759;10460;25613;21135;24891;18305;27415;12855;10899;24927;20670;22926;18006;23345;12602;12304;26622;19807;22747;14233;24736;10064;14169;35155;28962;33273;21796;35185;14877]
B =
20247
40182
36315
36518
26921
39185
16546
12094
25270
19330
18540
16386
21207
11759
10460
25613
21135
24891
18305
27415
12855
10899
24927
20670
22926
18006
23345
12602
12304
26622
19807
22747
14233
24736
10064
14169
35155
28962
33273
21796
35185
14877
>> A\B
ans =
102.0000
108.0000
97.0000
103.0000
123.0000
55.0000
101.0000
49.0000
55.0000
49.0000
100.0000
52.0000
51.0000
45.0000
54.0000
51.0000
98.0000
57.0000
45.0000
52.0000
101.0000
49.0000
56.0000
45.0000
57.0000
57.0000
48.0000
101.0000
45.0000
54.0000
101.0000
49.0000
52.0000
99.0000
50.0000
97.0000
102.0000
101.0000
54.0000
52.0000
56.0000
125.0000re-hyperthreading
就是简单的hook程序的执行流程,跳转到另一处地方进行加密。比较简单的汇编,不过多解释。
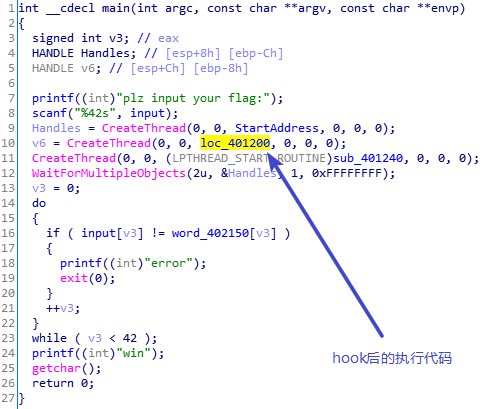
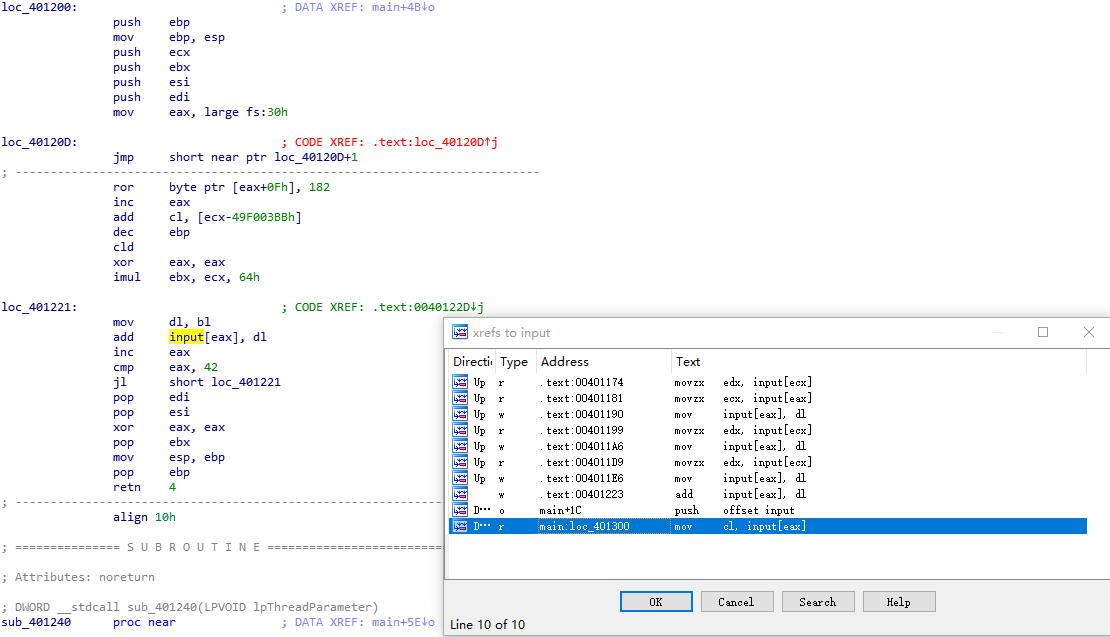
单击input,按x查看交叉引用。
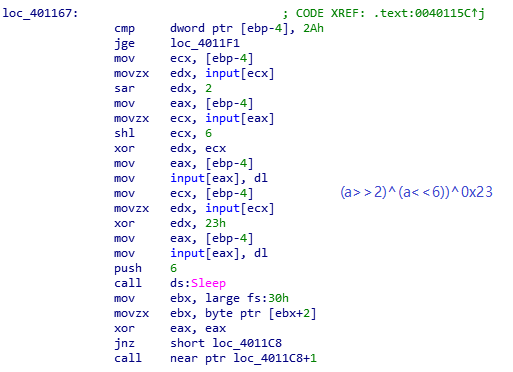
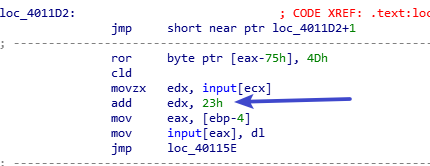
加密逻辑很简单,不多解释,dump出密文后运行下面的脚本:
with open(r'd:\dump','rb')as f:
b = f.read()
for i in b:
for a in range(127):
if ((((a>>2)^(a<<6))^0x23)+0x23)&0xff == i:
print(chr(a),end='')misc-电脑被黑
前面怎么搞的不清楚,拿到队友给出的密文和demo文件,逆向就行了,很简单。
def dec(i, n):
v4 = 34*(i+1)
v5 = (i*2) & 0xf
e = (n ^ v4) - v5
print(chr(e&0xff),end='')
with open(r'D:\文档\QQ文件\flag.txt','rb')as f:
b = f.read()
for i, n in enumerate(b):
dec(i, n)