LinkChecker
一个安卓题目,native+lua
assets目录下发现了lua脚本:
function check0(cipher)
local tbl = {}
local sum = 0;
local k = 220
for i=1, #cipher do
local x = string.byte(cipher, i)
sum = (sum * k + x) % 65537
tbl[i] = x
end
-- print(sum)
if sum == 16047 then
return libcheck.check1(tbl)
else
return 1
end
end
function check2(cipher)
local sum = 0;
local k = 39
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 18580 then
return libcheck.check3(cipher)
else
return 1
end
end
function check4(cipher)
local sum = 0;
local k = 4
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 1520 then
return libcheck.check5(cipher)
else
return 1
end
end
function check6(cipher)
local sum = 0;
local k = 137
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 8828 then
return libcheck.check7(cipher)
else
return 1
end
end
function check8(cipher)
local sum = 0;
local k = 211
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 53648 then
return libcheck.check9(cipher)
else
return 1
end
end
function check10(cipher)
local sum = 0;
local k = 238
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 32347 then
return libcheck.check11(cipher)
else
return 1
end
end
function check12(cipher)
local sum = 0;
local k = 133
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 45053 then
return libcheck.check13(cipher)
else
return 1
end
end
function check14(cipher)
local sum = 0;
local k = 179
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 14264 then
return libcheck.check15(cipher)
else
return 1
end
end
function check16(cipher)
local sum = 0;
local k = 158
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 25879 then
return libcheck.check17(cipher)
else
return 1
end
end
function check18(cipher)
local sum = 0;
local k = 40
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 7217 then
return libcheck.check19(cipher)
else
return 1
end
end
function check20(cipher)
local sum = 0;
local k = 196
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 17903 then
return libcheck.check21(cipher)
else
return 1
end
end
function check22(cipher)
local sum = 0;
local k = 248
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 46799 then
return libcheck.check23(cipher)
else
return 1
end
end
function check24(cipher)
local sum = 0;
local k = 157
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 55445 then
return libcheck.check25(cipher)
else
return 1
end
end
function check26(cipher)
local sum = 0;
local k = 163
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 11450 then
return libcheck.check27(cipher)
else
return 1
end
end
function check28(cipher)
local sum = 0;
local k = 167
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 11581 then
return libcheck.check29(cipher)
else
return 1
end
end
function check30(cipher)
local sum = 0;
local k = 159
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 50599 then
return libcheck.check31(cipher)
else
return 1
end
end
function check32(cipher)
local sum = 0;
local k = 29
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 38986 then
return libcheck.check33(cipher)
else
return 1
end
end
function check34(cipher)
local sum = 0;
local k = 93
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 39558 then
return libcheck.check35(cipher)
else
return 1
end
end
function check36(cipher)
local sum = 0;
local k = 8
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 61814 then
return libcheck.check37(cipher)
else
return 1
end
end
function check38(cipher)
local sum = 0;
local k = 81
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 41021 then
return libcheck.check39(cipher)
else
return 1
end
end
function check40(cipher)
local sum = 0;
local k = 181
for i=1, #cipher do
sum = (sum * k + cipher[i]) % 65537
end
-- print(sum)
if sum == 19105 then
return libcheck.check41(cipher)
else
return 1
end
end有check0,check2,check4,……,check40这些函数。
lib目录下有liblua.so,liblua.so,libcheck.so这三个native程序。
libcheck.so中有check1,check3,……,check41这些函数。
libcheck.so中的check函数是校验flag的函数,它调用lua脚本中的check0这个函数:
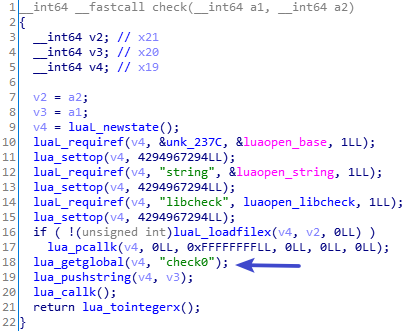
lua脚本中的check0函数又调用了libcheck.so中的check1函数,check1又调用了check.lua中的check2。这样一直调用到check41。中途验证失败则直接返回。
首先看一下lua中的check0,check2,check4,……,check40逻辑:
s = 0
for i in range(len(c))
s += (s * k + c[i]) % 65537
# k为常数比赛期间我觉得这个没法化简,一是取模,二是求和,这两个处我感觉都化不动简。其实是可以的。
首先:
(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p) % p
(a * b) % p = (a % p * b % p) % p
(a ^ b) % p = ((a % p) ^ b) % p所以在循环内部s += s * k + c[i]计算完之后,紧接着进行取模(这样的话需要进行21次取模运算);还是算出最后的sum之后再进行唯一一次取模,都是等价的。
在来看看我没化简出来的求和。其实就是高中的归纳法,一步一步带入即可。
s_init = 0
s0 = 0 * k + c0 = c0
s1 = c0 * k**1 + c1
s2 = (c0 * k + c1) * k + c2 = c0 * k**2 + c1 * k**1 + c2
s3 = (c0 * k**2 + c1 * k**1 + c2) * k + c3 = c0 * k**3 + c1 * k**2 + c2 * k**1 + c3
......
s(n-1) = c0 * k**(n-1) + c1 * k**(n-2) + c2 * k**(n-3) + ... + c(n-2) * k**1 + c(n-1)最终的sum即这里的s(n-1)
即:
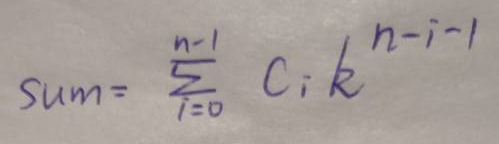
注意上下限哦~
是不是很简单。
再来归纳下libcheck.so中的check1,check3,……,check41的逻辑:
啊这,中间长长的一行是啥,把我看懵了。这个知识点会在“汇编除法取模优化”一文中展开来说,其实就是模65537。
因而逻辑可概括为:
s = 0
for i in range(len(c))
s += ((s + c[i]) * k) % 65537和之前的那个归纳类似,一层层往里带:
s_init = 0
s0 = c0 * k
s1 = (c0 * k + c1) * k = c0 * k**2 + c1 * k**1
s2 = (c0 * k**2 + c1 * k**1 + c2) * k = c0 * k**3 + c1 * k**2 + c2 * k**1
s3 = (c0 * k**3 + c1 * k**2 + c2 * k**1 + c3) * k = c0 * k**4 + c1 * k**3 + c2 * k**2 + c3 * k**1
......
s(n-1) = c0 * k**n + c1 * k**(n-1) + c2 * k**(n-2) + ... + c(n-1) * k**1即:
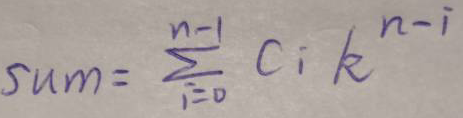
所以我们得到了两个逻辑式,分别可列21个方程,共42个。
但是,接下来的难点在于,题目的代码中的sum并不是表达式之和,而是表达式之和 % 65537.
如果没有取模的话,那么本题就是解一个线性方程组,非常简单。方程组中的一个方程类似是这样的:
c0 * k**n + c1 * k**(n-1) + c2 * k**(n-2) + ... + c(n-1) * k**1 = sum但现在的有取模的,方程组中的一个方程类似是这样的:
c0 * k**n + c1 * k**(n-1) + c2 * k**(n-2) + ... + c(n-1) * k**1 ≡ sum(mod 65537)这种方程是单模多元方程组。
github上居然解这种方程组的脚本:55-AA/mod_equations,注意是python2的。
按照上面归纳的逻辑式,用下面的脚本计算出相应的矩阵。上面的脚本要求的是一个增广矩阵(最后一列是方程右边的常数,对应本题的sum)
k = [220, 39, 4, 137, 211, 238, 133, 179, 158, 40, 196, 248, 157, 163, 167, 159,
29, 93, 8, 81, 181, 95, 171, 32, 101, 185, 184, 36, 160, 15, 207, 226, 9, 232,
109, 170, 176, 116, 213, 149, 19, 5]
sum = [16047, 18580, 1520, 8828, 53648, 32347, 45053, 14264, 25879, 7217, 17903,
46799, 55445, 11450, 11581, 50599, 38986, 39558, 61814, 41021, 19105, 13500,
58800, 47692, 58123, 50625, 9372, 18815, 40643, 30579, 51164, 64164, 18342,
48184, 45041, 49115, 4982, 33482, 25450, 18426, 31357, 38929]
n = len(k)
a = []
for i in range(21):
line = []
for j in range(n):
line.append(pow(k[i],n-j-1,65537))
a.append(line)
for i in range(21,42):
line = []
for j in range(n):
line.append(pow(k[i],n-j,65537))
a.append(line)
for line in range(len(a)):
a[line].append(sum[line]) # 变成增广矩阵
for i in range(len(a)):
print(a[i], end=',\n')在55-AA/mod_equations脚本中仿照原有的static_test_ex函数(不是static_test函数),增加一个solve_linkChecker函数。
注意,该脚本除了解单模多元线性方程组之外,还有别的功能,这些代码我都没删。
具体脚本如下:
#!/usr/bin/python
# -*- coding: utf-8 -*-
'''
Author @55-AA
19 July, 2016
'''
import copy
def gcd(a, b):
"""
Return the greatest common denominator of integers a and b.
gmpy2.gcd(a, b)
"""
while b:
a, b = b, a % b
return a
def lcm(a, b):
return a * b / (gcd(a, b))
def egcd(a, b):
"""
ax + by = 1
ax ≡ 1 mod b
Return a 3-element tuple (g, x, y), the g = gcd(a, b)
gmpy2.gcdext(a, b)
"""
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def mod_inv(a, m):
"""
ax ≡ 1 mod m
gmpy2.invert(a, m)
"""
g, x, y = egcd(a, m)
assert g == 1
return x % m
def int2mem(x):
"""
0x12233 => '\x33\x22\x01'
"""
pad_even = lambda x : ('', '0')[len(x)%2] + x
x = list(pad_even(format(x, 'x')).decode('hex'))
x.reverse()
return ''.join(x)
def mem2int(x):
"""
'\x33\x22\x01' => 0x12233
"""
x = list(x)
x.reverse()
return int(''.join(x).encode('hex'), 16)
###########################################################
# class
###########################################################
class GaussMatrix:
"""
A*X ≡ B (mod p),p为大于0的整数。
高斯消元求解模线性方程组。先化简为上三角,然后回代求解。
当r(A) <= n时,一定有多解;
当r(A) == n时,有多解或唯一解;
当r(A) != r(A~)时,无解。
r(A)为系数矩阵的秩,r(A)为增广矩阵的秩,n为未知数的个数。
http://www.docin.com/p-1063811671.html讨论了gcd(|A|, m) = 1时的LU分解解法,
本文包括了gcd(|A|, m) > 1时的解法,
化简原则:
1、系数与模互质
2、系数加某一行n次后,对应的系数与模的GCD最小
3、将1或2得到的系数移到对角线上
初始化参数:
matrix:方程组的增广矩阵(最后一列为常数项)。
matrix = [
[ 69, 75, 78, 36, 58],
[ 46, 68, 51, 26, 42],
[ 76, 40, 42, 49, 11],
[ 11, 45, 2, 45, 1],
[ 15, 67, 60, 14, 72],
[ 76, 67, 73, 56, 58],
[ 67, 15, 68, 54, 75],
]
mod:模数
函数:
gauss():求解方程
输出变量:
error_str:出错的信息
count:解的数量
"""
def __init__(self, matrix, mod):
self.matrix = copy.deepcopy(matrix)
self.d = None
self.r = len(matrix)
self.c = len(matrix[0])
self.N = len(matrix[0]) - 1
self.mod = mod
self.count = 1
self.error_str = "unknown error"
def verify_solution(self, solution):
for d in self.matrix:
result = 0
for r in map(lambda x,y:0 if None == y else x*y, d, solution):
result += r
if (result % self.mod) != ((d[-1]) % self.mod):
return 0
return 1
def swap_row(self, ra, rb):
(self.d[ra], self.d[rb]) = (self.d[rb], self.d[ra])
def swap_col(self, ca, cb):
for j in range(self.r):
(self.d[j][ca], self.d[j][cb]) = (self.d[j][cb], self.d[j][ca])
def inv_result(self, r, n):
"""
求解第n个未知数,r已经获得的解。形如:[None,None, ..., n+1, ...]
a*x ≡ b(mod m)
x有解的条件:gcd(a,m) | b。也即a,m互质时一定有解,不互质时,b整除gcd(a,m)也有解,否则无解。
解的格式为:x0+k(m/gcd(a,m)),其中x0为最小整数特解,k为任意整数。
返回[x0, x1, ...xn],其中x0 < x1 < xn < m。
"""
b = self.d[n][self.N]
a = self.d[n][n]
m = self.mod
k = gcd(a, m)
for j in xrange(n + 1, self.N):
b = (b - (self.d[n][j] * r[j] % m)) % m
if 1 == k:
return [mod_inv(a, m) * b % m]
else:
if k == gcd(k, b):
a /= k
b /= k
m /= k
x0 = mod_inv(a, m) * b % m
x = []
for i in xrange(k):
x.append(x0 + m*i)
return x
return None
def find_min_gcd_row_col(self, i, j):
# 查找直接互质的对角线系数
for k in xrange(i, self.r):
for l in xrange(j, self.c - 1):
if(1 == gcd(self.d[k][l], self.mod)):
return [k, l]
def add_min_gcd(a, b, m):
r = [m, 1]
g = gcd(a, b)
if g:
i = a / g
for j in xrange(i):
g = gcd((a + j * b) % m, m)
if g < r[0]:
r[0] = g
r[1] = j
if g == 1:
break
return r
# 查找加乘后GCD最小的对角线系数
# [加乘后的最大公约数,加乘的倍数,要化简的行号,加乘的行号,要化简的列号]
r = [self.mod, 1, i, i + 1, j]
for k in xrange(i, self.r):
for kk in xrange(k+1, self.r):
for l in range(j, self.c - 1):
rr = add_min_gcd(self.d[k][l], self.d[kk][l], self.mod)
if rr[0] < r[0]:
r[0] = rr[0]
r[1] = rr[1]
r[2] = k
r[3] = kk
r[4] = l
pass
if(1 == rr[0]):
break
g = r[0]
n = r[1]
k = r[2]
kk = r[3]
l = r[4]
if n and g < self.mod:
self.d[k] = map(lambda x, y : (x + n*y)%self.mod, self.d[k], self.d[kk])
return [k, l]
def mul_row(self, i, k, j):
a = self.d[k][j]
b = self.d[i][j]
def get_mul(a, b, m):
k = gcd(a, m)
if 1 == k:
return mod_inv(a, m) * b % m
else:
if k == gcd(k, b):
return mod_inv(a/k, m/k) * (b/k) % (m/k)
return None
if b:
mul = get_mul(a, b, self.mod)
if None == mul:
print_matrix(self.d)
assert(mul != None)
self.d[i] = map(lambda x, y : (y - x*mul) % self.mod, self.d[k], self.d[i])
def gauss(self):
"""
返回解向量,唯一解、多解或无解(None)。
例如:[[61, 25, 116, 164], [61, 60, 116, 94], [61, 95, 116, 24], [61, 130, 116, 129], [61, 165, 116, 59]]
"""
self.d = copy.deepcopy(self.matrix)
for i in xrange(self.r):
for j in xrange(self.c):
self.d[i][j] = self.matrix[i][j] % self.mod #把负系数变成正系数
if self.r < self.N:
self.d.extend([[0]*self.c]*(self.N - self.r))
# 化简上三角
index = [x for x in xrange(self.N)]
for i in range(self.N):
tmp = self.find_min_gcd_row_col(i, i)
if(tmp):
self.swap_row(i, tmp[0])
(index[i], index[tmp[1]]) = (index[tmp[1]], index[i])
self.swap_col(i, tmp[1])
else:
self.error_str = "no min"
return None
for k in range(i + 1, self.r):
self.mul_row(k, i, i)
# print_matrix(self.d)
if self.r > self.N:
for i in xrange(self.N, self.r):
for j in xrange(self.c):
if self.d[i][j]:
self.error_str = "r(A) != r(A~)"
return None
# 判断解的数量
for i in xrange(self.N):
self.count *= gcd(self.d[i][i], self.mod)
if self.count > 100:
self.error_str = "solution too more:%d" % (self.count)
return None
# 回代
result = [[None]*self.N]
for i in range(self.N - 1, -1, -1):
new_result = []
for r in result:
ret = self.inv_result(r, i)
if ret:
for rr in ret:
l = r[:]
l[i] = rr
new_result.append(l)
else:
self.error_str = "no inv:i=%d" % (i)
return None
result = new_result
# 调整列变换导致的未知数顺序变化
for i in xrange(len(result)) :
def xchg(a, b):
result[i][b] = a
map(xchg, result[i][:], index)
return result
###########################################################
# test
###########################################################
def print_array(x):
prn = "\t["
for j in x:
if j:
prn += "%3d, " % j
else:
prn += " 0, "
print prn[:-2]+"],"
def print_matrix(x):
print "["
for i in x:
print_array(i)
print "]"
def random_test(times):
import random
for i in xrange(times):
print "\n============== random test %d ==============\n" % i
mod = random.randint(5, 999)
col = random.randint(2, 30)
row = random.randint(2, 30)
solution = map(lambda x : random.randint(0, mod - 1), [xc for xc in xrange(col)])
matrix = []
for y in xrange(row):
array = map(lambda x : random.randint(0, mod), [xc for xc in xrange(col)])
t = 0
for j in map(lambda x,y:0 if None == y else x*y, array, solution):
t += j
array.append(t % mod)
matrix.append(array)
run_test(mod, solution, matrix)
def static_test_ex():
mod = 37
solution = [6, 10, 5, 11, 32, 39, 6, 42, 7, 18, 21, 8, 8, 27]
matrix = [
[ 32, 43, 11, 27, 14, 41, 27, 20, 0, 37, 7, 12, 9, 16, 12],
[ 23, 35, 31, 25, 46, 27, 48, 0, 4, 19, 43, 11, 31, 24, 36],
[ 48, 10, 47, 1, 42, 26, 0, 21, 10, 23, 7, 5, 13, 32, 41],
[ 15, 0, 6, 24, 6, 36, 4, 36, 18, 46, 33, 20, 4, 20, 39],
[ 4, 37, 3, 39, 26, 33, 13, 32, 23, 11, 45, 45, 29, 32, 35],
[ 38, 8, 38, 47, 1, 34, 36, 46, 47, 0, 22, 23, 21, 31, 21],
[ 21, 3, 17, 15, 46, 42, 7, 17, 12, 37, 30, 3, 14, 12, 16],
[ 7, 22, 14, 31, 31, 19, 34, 46, 9, 33, 12, 18, 4, 15, 32],
[ 13, 41, 35, 25, 19, 9, 44, 8, 0, 42, 15, 20, 3, 47, 29],
[ 36, 21, 36, 13, 37, 40, 21, 39, 2, 16, 26, 4, 15, 2, 23],
[ 41, 19, 28, 2, 42, 24, 27, 21, 21, 35, 3, 18, 7, 22, 36],
[ 42, 34, 17, 40, 26, 7, 14, 0, 7, 46, 30, 14, 34, 22, 39],
[ 18, 1, 40, 38, 17, 45, 24, 34, 34, 9, 32, 24, 9, 2, 45],
[ 43, 2, 1, 29, 47, 48, 28, 37, 10, 23, 35, 34, 37, 44, 35],
]
run_test(mod, solution, matrix)
def static_test():
mod = 26
solution = [23,15,19,13,25,17,24,18,11]
matrix = [
[11,12,7,0,0,0,0,0,0],
[0,0,0,11,12,7,0,0,0],
[0,0,0,0,0,0,11,12,7],
[14,18,23,0,0,0,0,0,0],
[0,0,0,14,18,23,0,0,0],
[0,0,0,0,0,0,14,18,23],
[17,5,19,0,0,0,0,0,0],
[0,0,0,17,5,19,0,0,0],
[0,0,0,0,0,0,17,5,19],
]
for i in xrange(len(matrix)):
t = 0
for j in map(lambda x,y:0 if None == y else x*y, matrix[i], solution):
t += j
matrix[i].append(t % mod)
run_test(mod, solution, matrix)
def solve_linkChecker():
mod = 65537
solution = []
matrix = [
[27436, 33489, 60625, 4744, 50068, 64573, 27402, 10253, 33113, 27259, 39744, 56185, 58345, 46439, 51747, 20790, 32863, 18321, 37916, 9705, 40260, 183, 47962, 40136, 15673, 9306, 6596, 51268, 28831, 23069, 36746, 54384, 26462, 57912, 55076, 9783, 24174, 5472, 31006, 48400, 220, 1, 16047],
[5092, 1811, 63903, 41969, 4437, 20279, 39170, 49737, 61771, 63760, 63811, 58771, 13270, 7062, 15305, 64249, 38617, 58125, 11573, 59112, 6557, 3529, 52184, 55112, 4774, 37092, 16075, 57547, 3156, 50494, 33223, 63028, 43627, 17923, 2140, 62231, 45287, 19646, 59319, 1521, 39, 1, 18580],
[65533, 65536, 16384, 4096, 1024, 256, 64, 16, 4, 1, 49153, 61441, 64513, 65281, 65473, 65521, 65533, 65536, 16384, 4096, 1024, 256, 64, 16, 4, 1, 49153, 61441, 64513, 65281, 65473, 65521, 65533, 65536, 16384, 4096, 1024, 256, 64, 16, 4, 1, 1520],
[46431, 50568, 19504, 20234, 12107, 65147, 26786, 47076, 21392, 47515, 35268, 31830, 37067, 54805, 28624, 54265, 60671, 18621, 29795, 18874, 3008, 57905, 29125, 38004, 48593, 12314, 1525, 22973, 32697, 28941, 21738, 8291, 46941, 45788, 38604, 27549, 15509, 13986, 15410, 18769, 137, 1, 8828],
[6960, 35131, 16939, 52572, 7393, 59360, 45008, 48046, 48371, 25388, 12855, 12485, 37642, 489, 46282, 41840, 17592, 37045, 38069, 29377, 28404, 30263, 61332, 21101, 32092, 50159, 13283, 7828, 16499, 1010, 2179, 44737, 29098, 15668, 23680, 28377, 18460, 18413, 22140, 44521, 211, 1, 53648],
[24540, 10567, 8030, 50701, 48402, 25537, 48847, 18104, 16598, 50737, 52808, 4077, 7452, 60061, 14296, 16582, 34215, 47782, 7911, 17932, 2829, 29476, 61255, 51200, 47578, 26635, 52156, 18944, 32022, 52454, 48134, 43710, 62967, 49555, 61064, 9619, 44925, 47827, 46187, 56644, 238, 1, 32347],
[41110, 47614, 358, 42380, 5739, 57696, 36898, 56452, 42309, 59942, 42828, 12641, 37052, 21960, 59789, 50711, 37831, 3241, 6923, 10400, 29151, 16973, 46447, 54060, 54610, 34411, 40665, 26422, 17938, 59266, 7837, 4001, 35016, 64322, 20194, 61254, 63041, 27083, 58842, 17689, 133, 1, 45053],
[46452, 38703, 16692, 39269, 39029, 48547, 56655, 38760, 35731, 1298, 39183, 63193, 23053, 9282, 54605, 59984, 28527, 53248, 16041, 1188, 38084, 12295, 6659, 5163, 3324, 58233, 44993, 2082, 12460, 41076, 15973, 27915, 31643, 23609, 37477, 53298, 52288, 54113, 33620, 32041, 179, 1, 14264],
[475, 37749, 33837, 26346, 63215, 42294, 13541, 61060, 31081, 5589, 64328, 44375, 49641, 46356, 46750, 41775, 18930, 47406, 30165, 33789, 49574, 7780, 58120, 11982, 1735, 17847, 63576, 36904, 54986, 10303, 480, 29868, 30054, 38351, 15590, 3417, 1266, 9963, 12092, 24964, 158, 1, 25879],
[8368, 26424, 13768, 26559, 54732, 7922, 23136, 53008, 27540, 33457, 64735, 42579, 22364, 46435, 9353, 51025, 25852, 7200, 180, 32773, 18842, 23409, 38269, 5872, 39469, 5902, 55854, 30888, 26987, 48189, 6120, 153, 50795, 9462, 55943, 3037, 31206, 4057, 64000, 1600, 40, 1, 7217],
[45752, 56408, 39075, 31296, 22897, 58632, 19024, 8122, 24785, 10492, 4066, 64889, 25409, 34570, 16895, 9783, 37834, 36974, 51682, 57107, 31388, 18885, 62624, 1657, 10374, 23459, 8479, 17765, 34531, 7198, 62230, 33086, 7525, 2379, 1684, 12046, 27480, 26890, 58318, 38416, 196, 1, 17903],
[27648, 55078, 9207, 57382, 2874, 41765, 62270, 9236, 60289, 25348, 39213, 3065, 63171, 22717, 57965, 11597, 32551, 10966, 28056, 19140, 18047, 21478, 19642, 50289, 10509, 41003, 31084, 58263, 61808, 17162, 50279, 467, 62632, 31964, 24441, 59029, 5259, 11913, 48408, 61504, 248, 1, 46799],
[14810, 61457, 25020, 58600, 30011, 38595, 55347, 56706, 35843, 64513, 21700, 32698, 1878, 55948, 46274, 11148, 12594, 32640, 61988, 55496, 22060, 18925, 15983, 5111, 40941, 8192, 23011, 564, 50513, 11175, 23030, 41890, 30322, 1028, 28392, 14791, 20131, 45211, 3210, 24649, 157, 1, 55445],
[25071, 60866, 27714, 53645, 11587, 23391, 15020, 58794, 49815, 26440, 28709, 35156, 25948, 4984, 44258, 38870, 33208, 1812, 41022, 32015, 27537, 30324, 47630, 28839, 36363, 23543, 15423, 55982, 9591, 12925, 51946, 55804, 22054, 16218, 50760, 27652, 43995, 12734, 5305, 26569, 163, 1, 11450],
[64293, 53364, 47412, 30894, 59443, 9382, 57352, 52930, 9343, 9082, 8688, 25168, 20165, 64088, 11372, 34995, 53581, 33678, 41800, 52052, 1489, 43177, 47351, 41097, 28894, 19010, 20913, 42116, 4569, 49082, 30904, 56696, 62737, 48253, 3036, 57314, 10939, 3205, 4336, 27889, 167, 1, 11581],
[61034, 34595, 41848, 56320, 42809, 24588, 61982, 61805, 12342, 9970, 16550, 2165, 14440, 503, 13193, 18219, 37211, 43101, 11400, 21093, 48358, 31630, 50073, 54723, 9000, 23551, 45076, 35319, 36082, 50101, 58845, 63434, 32137, 45130, 52631, 56800, 29210, 12137, 21922, 25281, 159, 1, 50599],
[36239, 14809, 36669, 32903, 57632, 8767, 7082, 4764, 49882, 46918, 42296, 55696, 35819, 26094, 61917, 47333, 49090, 40111, 26242, 64182, 49671, 62730, 4423, 11452, 63672, 58693, 65301, 40670, 10442, 45558, 44509, 62552, 45095, 1555, 13613, 9509, 63605, 51911, 24389, 841, 29, 1, 38986],
[62067, 57748, 30923, 3856, 40914, 23695, 55926, 36541, 9554, 20539, 32637, 23606, 18576, 27683, 43989, 473, 56381, 31613, 16548, 23433, 44648, 56856, 36551, 14487, 48780, 11095, 824, 39472, 20156, 20653, 49551, 4761, 61360, 56331, 6948, 6417, 69, 27484, 17913, 8649, 93, 1, 39558],
[63489, 65281, 65505, 65533, 32768, 4096, 512, 64, 8, 1, 57345, 64513, 65409, 65521, 65535, 16384, 2048, 256, 32, 4, 32769, 61441, 65025, 65473, 65529, 65536, 8192, 1024, 128, 16, 2, 49153, 63489, 65281, 65505, 65533, 32768, 4096, 512, 64, 8, 1, 61814],
[31249, 59450, 33907, 3655, 15418, 30127, 25454, 31060, 37602, 15028, 20413, 8343, 103, 46929, 46698, 12713, 33330, 53812, 30601, 59442, 34716, 61111, 37973, 2087, 42908, 19139, 55255, 40328, 50662, 37844, 6940, 51868, 30577, 61869, 10473, 63239, 19390, 54449, 7145, 6561, 81, 1, 41021],
[11224, 8752, 15980, 29417, 19715, 4816, 19217, 3727, 6176, 30087, 47237, 48418, 2440, 50343, 43366, 6395, 64124, 20993, 52618, 32154, 49783, 35035, 50161, 39020, 63218, 16643, 26524, 32734, 13940, 13112, 19987, 6990, 27919, 64605, 13754, 56923, 59334, 49209, 31411, 32761, 181, 1, 19105],
[17028, 21565, 227, 37255, 31436, 60349, 37198, 18328, 25028, 63041, 64131, 26200, 24421, 25782, 37524, 50755, 52274, 37113, 39023, 59739, 19945, 55399, 16450, 31217, 13436, 32565, 24488, 59586, 57196, 26127, 30629, 2392, 61423, 18583, 28480, 24445, 62345, 52396, 53671, 5394, 9025, 95, 13500],
[39257, 61934, 29873, 42333, 23243, 43444, 62725, 36393, 9411, 50645, 4512, 32220, 17435, 28463, 15880, 46467, 14069, 24994, 17776, 41879, 18258, 64494, 31421, 52690, 32885, 10157, 5425, 40657, 25916, 36561, 49654, 59312, 8012, 7712, 34155, 13997, 7747, 23424, 40379, 19399, 29241, 171, 58800],
[65533, 8192, 256, 8, 49153, 65025, 65521, 32768, 1024, 32, 1, 63489, 65473, 65535, 4096, 128, 4, 57345, 65281, 65529, 16384, 512, 16, 32769, 64513, 65505, 65536, 2048, 64, 2, 61441, 65409, 65533, 8192, 256, 8, 49153, 65025, 65521, 32768, 1024, 32, 47692],
[60301, 22659, 29424, 18460, 37169, 38652, 58782, 582, 64245, 17507, 56626, 36898, 18534, 52094, 10249, 2697, 31173, 63899, 9717, 17616, 35214, 36686, 28914, 23646, 883, 53217, 10909, 38392, 1029, 6499, 29264, 53498, 20645, 62497, 10352, 13729, 59833, 62885, 53182, 47246, 10201, 101, 58123],
[54253, 43158, 62582, 19468, 23486, 4378, 7463, 35820, 55103, 13051, 39747, 35286, 45181, 2724, 24104, 40161, 36351, 905, 53143, 43152, 65416, 13461, 64547, 8851, 57437, 24754, 17138, 53585, 9146, 27327, 3336, 62721, 63042, 42497, 3418, 2144, 57755, 5626, 7824, 40073, 34225, 185, 50625],
[35358, 23700, 24349, 61039, 40580, 13043, 36045, 63952, 3197, 40978, 36553, 42584, 62919, 6397, 58092, 64428, 61613, 18500, 12923, 7550, 17850, 27879, 9056, 31393, 62502, 46643, 19131, 61723, 39159, 569, 39539, 36189, 32609, 45412, 24467, 61752, 48776, 25910, 52143, 3489, 33856, 184, 9372],
[34377, 28262, 4426, 62019, 18107, 31451, 9976, 7559, 31158, 33634, 19139, 9634, 40318, 63016, 30878, 48190, 41389, 13893, 27693, 49922, 48719, 54147, 39734, 48436, 30473, 64563, 61869, 7180, 29327, 9917, 63992, 38187, 17445, 5946, 11088, 308, 36418, 41062, 41191, 46656, 1296, 36, 18815],
[18514, 32065, 39113, 62095, 59781, 11433, 61922, 38890, 61684, 44623, 33457, 32568, 55910, 37214, 40374, 56778, 35581, 27666, 58337, 65492, 18432, 26330, 28837, 24347, 28415, 26802, 5902, 46732, 34699, 21926, 50109, 1542, 63089, 58968, 56075, 35167, 53059, 38425, 55537, 32706, 25600, 160, 40643],
[50011, 33918, 28476, 54328, 7991, 9271, 31202, 63248, 52277, 64653, 30525, 2035, 43827, 42244, 59615, 25820, 23567, 62739, 17290, 44844, 16097, 62241, 56579, 38725, 46273, 7454, 35450, 24209, 36567, 41760, 2784, 13293, 27101, 10545, 703, 4416, 52724, 38468, 50625, 3375, 225, 15, 30579],
[52346, 26531, 2661, 44654, 55938, 46811, 37902, 41025, 1148, 4438, 45929, 26500, 64082, 35136, 54309, 52502, 30331, 6162, 19026, 39984, 36286, 25187, 10253, 54822, 29709, 22939, 47918, 9413, 59567, 36064, 14738, 32998, 15673, 7041, 15231, 18120, 38080, 3350, 17746, 22248, 42849, 207, 51164],
[43752, 34992, 40173, 16707, 42122, 30345, 49722, 22259, 10828, 41806, 21644, 16915, 40383, 37007, 60191, 7516, 49331, 6308, 41786, 63402, 33919, 45678, 24561, 14898, 63863, 34791, 20743, 17201, 46184, 29783, 17241, 28205, 61312, 6651, 53097, 20824, 25031, 16640, 57491, 8664, 51076, 226, 64164],
[34716, 25703, 61111, 14072, 37973, 18783, 2087, 58487, 42908, 41177, 19139, 38536, 55255, 35267, 40328, 62736, 50662, 12911, 37844, 62460, 6940, 8053, 51868, 13045, 30577, 32525, 61869, 28720, 10473, 44855, 63239, 43436, 19390, 31282, 54449, 64305, 7145, 59049, 6561, 729, 81, 9, 18342],
[16969, 35949, 10042, 6258, 64999, 36721, 60893, 21449, 42748, 5834, 46918, 5287, 50023, 2758, 41255, 7240, 4551, 2562, 44644, 53300, 60117, 57604, 28497, 29219, 53516, 14920, 6844, 32798, 30085, 25836, 8021, 23481, 15638, 52610, 60679, 23143, 27501, 966, 25428, 35138, 53824, 232, 48184],
[52969, 26340, 52551, 11906, 1913, 17454, 32628, 58020, 18570, 55486, 40192, 45463, 14246, 26586, 51952, 55191, 58227, 49236, 47951, 7655, 1874, 48719, 47345, 34706, 8736, 9099, 45779, 44913, 40095, 35842, 59252, 57663, 42617, 23840, 3225, 36105, 23179, 52522, 57000, 49826, 11881, 109, 45041],
[1473, 27380, 31002, 21000, 15544, 18596, 20156, 47151, 37672, 13329, 35931, 37606, 58819, 16923, 31326, 24086, 43319, 55383, 23842, 24813, 50648, 2611, 37410, 31061, 26012, 32536, 20238, 64114, 61288, 48935, 21491, 2825, 28930, 27156, 8641, 22025, 63739, 51648, 6472, 63262, 28900, 170, 49115],
[52370, 53174, 57647, 60279, 57315, 34956, 7646, 12704, 11988, 40284, 25550, 60469, 46145, 53511, 27487, 36276, 40422, 27785, 32554, 14335, 54075, 8127, 36166, 15845, 10144, 41763, 11036, 13468, 1566, 42459, 8061, 60742, 57690, 2562, 52891, 25994, 61961, 44664, 50896, 12205, 30976, 176, 4982],
[28113, 51655, 50728, 7217, 26616, 31868, 16094, 60026, 10687, 2917, 46918, 10574, 3481, 22064, 4710, 35069, 29116, 251, 25426, 26208, 20565, 6392, 2315, 20924, 52158, 58077, 58693, 65478, 10734, 55460, 2738, 35052, 47760, 16231, 63982, 12981, 19886, 53279, 50742, 53545, 13456, 116, 33482],
[58637, 6429, 46183, 57754, 3348, 4631, 64328, 11071, 5898, 37873, 8793, 60963, 13209, 48984, 33460, 4157, 2481, 22165, 37334, 22944, 4723, 35406, 62011, 19983, 19478, 20091, 11171, 20052, 30555, 58296, 38119, 22640, 6260, 20952, 26867, 57971, 24887, 13655, 25602, 29658, 45369, 213, 25450],
[40009, 47332, 42103, 27553, 62643, 32969, 32330, 48600, 17920, 32229, 60915, 48352, 41670, 42065, 6880, 17640, 4077, 46651, 14828, 47163, 58816, 39541, 58325, 50094, 40802, 59653, 41306, 57897, 27659, 13381, 30879, 9444, 63841, 1748, 33440, 38491, 18292, 62141, 46161, 31099, 22201, 149, 18426],
[45080, 61011, 23907, 52998, 9688, 45351, 47228, 5935, 7211, 38322, 57206, 37504, 46815, 57653, 9933, 24668, 63386, 24032, 35758, 1882, 10447, 35043, 8743, 31504, 22354, 39119, 46900, 19715, 59676, 37634, 15778, 18077, 18198, 25103, 42713, 12596, 55852, 51230, 64784, 6859, 361, 19, 31357],
[28140, 5628, 14233, 15954, 42513, 21610, 4322, 53294, 49981, 36211, 33457, 59121, 38039, 46930, 9386, 28092, 58048, 24717, 57373, 24582, 57346, 37684, 46859, 48694, 49061, 36027, 59635, 11927, 54815, 10963, 15300, 3060, 612, 52552, 62940, 12588, 15625, 3125, 625, 125, 25, 5, 38929],
]
run_test(mod, solution, matrix)
def run_test(mod, solution, matrix):
print "row = %d, col = %d" % (len(matrix), len(matrix[0])-1)
print "mod = %d" % (mod)
print "solution =", solution
print "matrix ="
print_matrix(matrix)
g = GaussMatrix(matrix, mod)
ret = g.gauss()
if not ret:
print "error:"
print_matrix(g.d)
print "error_str:", g.error_str
else:
print "times:", g.count
print "result:"
print_matrix(ret)
def DSA_comK():
"""
# DSA两次签名使用相同的随机数k可导致私钥x泄漏
# p:L bits长的素数。L是64的倍数,范围是512到1024;
# q:p - 1的160bits的素因子;
# g:g = h^((p-1)/q) mod p,h满足h < p - 1, h^((p-1)/q) mod p > 1;
# x:x < q,x为私钥 ;
# y:y = g^x mod p ,( p, q, g, y )为公钥;
# r = ( g^k mod p ) mod q
# s = ( k^(-1) (HASH(m) + xr)) mod q
# 签名结果是( m, r, s )
"""
import hashlib
p = 0x8c286991e30fd5341b7832ce9fe869c0a73cf79303c2959ab677d980237abf7ecf853015c9a086c4330252043525a4fa60c64397421caa290225d6bc6ec6b122cd1da4bba1b13f51daca8b210156a28a0c3dbf17a7826f738fdfa87b22d7df990908c13dbd0a1709bbbab5f816ddba6c8166ef5696414538f6780fdce987552b
g = 0x49874582cd9af51d6f554c8fae68588c383272c357878d7f4079c6edcda3bcbf1f2cbada3f7d541a5b1ae7f046199f8f51d72db60a2601bd3375a3b48d7a3c9a0c0e4e8a0680f7fb98a8610f042e10340d2453d3c811088e48c5d6dd834eaa5509daeb430bcd9de8aabc239d698a655004e3f0a2ee456ffe9331c5f32c66f90d
q = 0x843437e860962d85d17d6ee4dd2c43bc4aec07a5
m1 = 0x3132333435363738
r1 = 0x4d91a491d95e4eef4196a583cd282ca0e625f36d
s1 = 0x3639b47678abf7545397fc9a1af108537fd1dfac
m2 = 0x49276c6c206265206261636b2e
r2 = 0x4d91a491d95e4eef4196a583cd282ca0e625f36d
s2 = 0x314c044409a94f4961340212b42ade005fb27b0a
# M1 = mem2int(hashlib.sha1(int2mem(m1)).digest())
M1 = int(hashlib.sha1('3132333435363738'.decode('hex')).hexdigest(), 16)
# M2 = mem2int(hashlib.sha1(int2mem(m2)).digest())
M2 = int(hashlib.sha1('49276c6c206265206261636b2e'.decode("hex")).hexdigest(), 16)
matrix_c = [
[0x3639b47678abf7545397fc9a1af108537fd1dfac, -0x4d91a491d95e4eef4196a583cd282ca0e625f36d, M1],
[0x314c044409a94f4961340212b42ade005fb27b0a, -0x4d91a491d95e4eef4196a583cd282ca0e625f36d, M2]
]
print "mod = %d" % (q)
print "matrix ="
print_matrix(matrix_c)
Gauss = GaussMatrix(matrix_c, q)
ret = Gauss.gauss()
if not ret:
print "error:"
print_matrix(Gauss.d)
print "error_str:", Gauss.error_str
else:
k = ret[0][0]
x = ret[0][1]
print "k: %x" % (k)
print "x: %x" % (x)
print Gauss.verify_solution(ret[0])
if __name__ == "__main__":
# DSA_comK()
# static_test()
# static_test_ex()
#random_test(1)
#exit(0)
solve_linkChecker()python2运行:
D:\桌面\1>python2 mod-final.py
row = 42, col = 42
mod = 65537
solution = []
matrix =
[
[27436, 33489, 60625, 4744, 50068, 64573, 27402, 10253, 33113, 27259, 39744, 56185, 58345, 46439, 51747, 20790, 32863, 18321, 37916, 9705, 40260, 183, 47962, 40136, 15673, 9306, 6596, 51268, 28831, 23069, 36746, 54384, 26462, 57912, 55076, 9783, 24174, 5472, 31006, 48400, 220, 1, 16047],
[5092, 1811, 63903, 41969, 4437, 20279, 39170, 49737, 61771, 63760, 63811, 58771, 13270, 7062, 15305, 64249, 38617, 58125, 11573, 59112, 6557, 3529, 52184, 55112, 4774, 37092, 16075, 57547, 3156, 50494, 33223, 63028, 43627, 17923, 2140, 62231, 45287, 19646, 59319, 1521, 39, 1, 18580],
[65533, 65536, 16384, 4096, 1024, 256, 64, 16, 4, 1, 49153, 61441, 64513, 65281, 65473, 65521, 65533, 65536, 16384, 4096, 1024, 256, 64, 16, 4, 1, 49153, 61441, 64513, 65281, 65473, 65521, 65533, 65536, 16384, 4096, 1024, 256, 64, 16, 4, 1, 1520],
[46431, 50568, 19504, 20234, 12107, 65147, 26786, 47076, 21392, 47515, 35268, 31830, 37067, 54805, 28624, 54265, 60671, 18621, 29795, 18874, 3008, 57905, 29125, 38004, 48593, 12314, 1525, 22973, 32697, 28941, 21738, 8291, 46941, 45788, 38604, 27549, 15509, 13986, 15410, 18769, 137, 1, 8828],
[6960, 35131, 16939, 52572, 7393, 59360, 45008, 48046, 48371, 25388, 12855, 12485, 37642, 489, 46282, 41840, 17592, 37045, 38069, 29377, 28404, 30263, 61332, 21101, 32092, 50159, 13283, 7828, 16499, 1010, 2179, 44737, 29098, 15668, 23680, 28377, 18460, 18413, 22140, 44521, 211, 1, 53648],
[24540, 10567, 8030, 50701, 48402, 25537, 48847, 18104, 16598, 50737, 52808, 4077, 7452, 60061, 14296, 16582, 34215, 47782, 7911, 17932, 2829, 29476, 61255, 51200, 47578, 26635, 52156, 18944, 32022, 52454, 48134, 43710, 62967, 49555, 61064, 9619, 44925, 47827, 46187, 56644, 238, 1, 32347],
[41110, 47614, 358, 42380, 5739, 57696, 36898, 56452, 42309, 59942, 42828, 12641, 37052, 21960, 59789, 50711, 37831, 3241, 6923, 10400, 29151, 16973, 46447, 54060, 54610, 34411, 40665, 26422, 17938, 59266, 7837, 4001, 35016, 64322, 20194, 61254, 63041, 27083, 58842, 17689, 133, 1, 45053],
[46452, 38703, 16692, 39269, 39029, 48547, 56655, 38760, 35731, 1298, 39183, 63193, 23053, 9282, 54605, 59984, 28527, 53248, 16041, 1188, 38084, 12295, 6659, 5163, 3324, 58233, 44993, 2082, 12460, 41076, 15973, 27915, 31643, 23609, 37477, 53298, 52288, 54113, 33620, 32041, 179, 1, 14264],
[475, 37749, 33837, 26346, 63215, 42294, 13541, 61060, 31081, 5589, 64328, 44375, 49641, 46356, 46750, 41775, 18930, 47406, 30165, 33789, 49574, 7780, 58120, 11982, 1735, 17847, 63576, 36904, 54986, 10303, 480, 29868, 30054, 38351, 15590, 3417, 1266, 9963, 12092, 24964, 158, 1, 25879],
[8368, 26424, 13768, 26559, 54732, 7922, 23136, 53008, 27540, 33457, 64735, 42579, 22364, 46435, 9353, 51025, 25852, 7200, 180, 32773, 18842, 23409, 38269, 5872, 39469, 5902, 55854, 30888, 26987, 48189, 6120, 153, 50795, 9462, 55943, 3037, 31206, 4057, 64000, 1600, 40, 1, 7217],
[45752, 56408, 39075, 31296, 22897, 58632, 19024, 8122, 24785, 10492, 4066, 64889, 25409, 34570, 16895, 9783, 37834, 36974, 51682, 57107, 31388, 18885, 62624, 1657, 10374, 23459, 8479, 17765, 34531, 7198, 62230, 33086, 7525, 2379, 1684, 12046, 27480, 26890, 58318, 38416, 196, 1, 17903],
[27648, 55078, 9207, 57382, 2874, 41765, 62270, 9236, 60289, 25348, 39213, 3065, 63171, 22717, 57965, 11597, 32551, 10966, 28056, 19140, 18047, 21478, 19642, 50289, 10509, 41003, 31084, 58263, 61808, 17162, 50279, 467, 62632, 31964, 24441, 59029, 5259, 11913, 48408, 61504, 248, 1, 46799],
[14810, 61457, 25020, 58600, 30011, 38595, 55347, 56706, 35843, 64513, 21700, 32698, 1878, 55948, 46274, 11148, 12594, 32640, 61988, 55496, 22060, 18925, 15983, 5111, 40941, 8192, 23011, 564, 50513, 11175, 23030, 41890, 30322, 1028, 28392, 14791, 20131, 45211, 3210, 24649, 157, 1, 55445],
[25071, 60866, 27714, 53645, 11587, 23391, 15020, 58794, 49815, 26440, 28709, 35156, 25948, 4984, 44258, 38870, 33208, 1812, 41022, 32015, 27537, 30324, 47630, 28839, 36363, 23543, 15423, 55982, 9591, 12925, 51946, 55804, 22054, 16218, 50760, 27652, 43995, 12734, 5305, 26569, 163, 1, 11450],
[64293, 53364, 47412, 30894, 59443, 9382, 57352, 52930, 9343, 9082, 8688, 25168, 20165, 64088, 11372, 34995, 53581, 33678, 41800, 52052, 1489, 43177, 47351, 41097, 28894, 19010, 20913, 42116, 4569, 49082, 30904, 56696, 62737, 48253, 3036, 57314, 10939, 3205, 4336, 27889, 167, 1, 11581],
[61034, 34595, 41848, 56320, 42809, 24588, 61982, 61805, 12342, 9970, 16550, 2165, 14440, 503, 13193, 18219, 37211, 43101, 11400, 21093, 48358, 31630, 50073, 54723, 9000, 23551, 45076, 35319, 36082, 50101, 58845, 63434, 32137, 45130, 52631, 56800, 29210, 12137, 21922, 25281, 159, 1, 50599],
[36239, 14809, 36669, 32903, 57632, 8767, 7082, 4764, 49882, 46918, 42296, 55696, 35819, 26094, 61917, 47333, 49090, 40111, 26242, 64182, 49671, 62730, 4423, 11452, 63672, 58693, 65301, 40670, 10442, 45558, 44509, 62552, 45095, 1555, 13613, 9509, 63605, 51911, 24389, 841, 29, 1, 38986],
[62067, 57748, 30923, 3856, 40914, 23695, 55926, 36541, 9554, 20539, 32637, 23606, 18576, 27683, 43989, 473, 56381, 31613, 16548, 23433, 44648, 56856, 36551, 14487, 48780, 11095, 824, 39472, 20156, 20653, 49551, 4761, 61360, 56331, 6948, 6417, 69, 27484, 17913, 8649, 93, 1, 39558],
[63489, 65281, 65505, 65533, 32768, 4096, 512, 64, 8, 1, 57345, 64513, 65409, 65521, 65535, 16384, 2048, 256, 32, 4, 32769, 61441, 65025, 65473, 65529, 65536, 8192, 1024, 128, 16, 2, 49153, 63489, 65281, 65505, 65533, 32768, 4096, 512, 64, 8, 1, 61814],
[31249, 59450, 33907, 3655, 15418, 30127, 25454, 31060, 37602, 15028, 20413, 8343, 103, 46929, 46698, 12713, 33330, 53812, 30601, 59442, 34716, 61111, 37973, 2087, 42908, 19139, 55255, 40328, 50662, 37844, 6940, 51868, 30577, 61869, 10473, 63239, 19390, 54449, 7145, 6561, 81, 1, 41021],
[11224, 8752, 15980, 29417, 19715, 4816, 19217, 3727, 6176, 30087, 47237, 48418, 2440, 50343, 43366, 6395, 64124, 20993, 52618, 32154, 49783, 35035, 50161, 39020, 63218, 16643, 26524, 32734, 13940, 13112, 19987, 6990, 27919, 64605, 13754, 56923, 59334, 49209, 31411, 32761, 181, 1, 19105],
[17028, 21565, 227, 37255, 31436, 60349, 37198, 18328, 25028, 63041, 64131, 26200, 24421, 25782, 37524, 50755, 52274, 37113, 39023, 59739, 19945, 55399, 16450, 31217, 13436, 32565, 24488, 59586, 57196, 26127, 30629, 2392, 61423, 18583, 28480, 24445, 62345, 52396, 53671, 5394, 9025, 95, 13500],
[39257, 61934, 29873, 42333, 23243, 43444, 62725, 36393, 9411, 50645, 4512, 32220, 17435, 28463, 15880, 46467, 14069, 24994, 17776, 41879, 18258, 64494, 31421, 52690, 32885, 10157, 5425, 40657, 25916, 36561, 49654, 59312, 8012, 7712, 34155, 13997, 7747, 23424, 40379, 19399, 29241, 171, 58800],
[65533, 8192, 256, 8, 49153, 65025, 65521, 32768, 1024, 32, 1, 63489, 65473, 65535, 4096, 128, 4, 57345, 65281, 65529, 16384, 512, 16, 32769, 64513, 65505, 65536, 2048, 64, 2, 61441, 65409, 65533, 8192, 256, 8, 49153, 65025, 65521, 32768, 1024, 32, 47692],
[60301, 22659, 29424, 18460, 37169, 38652, 58782, 582, 64245, 17507, 56626, 36898, 18534, 52094, 10249, 2697, 31173, 63899, 9717, 17616, 35214, 36686, 28914, 23646, 883, 53217, 10909, 38392, 1029, 6499, 29264, 53498, 20645, 62497, 10352, 13729, 59833, 62885, 53182, 47246, 10201, 101, 58123],
[54253, 43158, 62582, 19468, 23486, 4378, 7463, 35820, 55103, 13051, 39747, 35286, 45181, 2724, 24104, 40161, 36351, 905, 53143, 43152, 65416, 13461, 64547, 8851, 57437, 24754, 17138, 53585, 9146, 27327, 3336, 62721, 63042, 42497, 3418, 2144, 57755, 5626, 7824, 40073, 34225, 185, 50625],
[35358, 23700, 24349, 61039, 40580, 13043, 36045, 63952, 3197, 40978, 36553, 42584, 62919, 6397, 58092, 64428, 61613, 18500, 12923, 7550, 17850, 27879, 9056, 31393, 62502, 46643, 19131, 61723, 39159, 569, 39539, 36189, 32609, 45412, 24467, 61752, 48776, 25910, 52143, 3489, 33856, 184, 9372],
[34377, 28262, 4426, 62019, 18107, 31451, 9976, 7559, 31158, 33634, 19139, 9634, 40318, 63016, 30878, 48190, 41389, 13893, 27693, 49922, 48719, 54147, 39734, 48436, 30473, 64563, 61869, 7180, 29327, 9917, 63992, 38187, 17445, 5946, 11088, 308, 36418, 41062, 41191, 46656, 1296, 36, 18815],
[18514, 32065, 39113, 62095, 59781, 11433, 61922, 38890, 61684, 44623, 33457, 32568, 55910, 37214, 40374, 56778, 35581, 27666, 58337, 65492, 18432, 26330, 28837, 24347, 28415, 26802, 5902, 46732, 34699, 21926, 50109, 1542, 63089, 58968, 56075, 35167, 53059, 38425, 55537, 32706, 25600, 160, 40643],
[50011, 33918, 28476, 54328, 7991, 9271, 31202, 63248, 52277, 64653, 30525, 2035, 43827, 42244, 59615, 25820, 23567, 62739, 17290, 44844, 16097, 62241, 56579, 38725, 46273, 7454, 35450, 24209, 36567, 41760, 2784, 13293, 27101, 10545, 703, 4416, 52724, 38468, 50625, 3375, 225, 15, 30579],
[52346, 26531, 2661, 44654, 55938, 46811, 37902, 41025, 1148, 4438, 45929, 26500, 64082, 35136, 54309, 52502, 30331, 6162, 19026, 39984, 36286, 25187, 10253, 54822, 29709, 22939, 47918, 9413, 59567, 36064, 14738, 32998, 15673, 7041, 15231, 18120, 38080, 3350, 17746, 22248, 42849, 207, 51164],
[43752, 34992, 40173, 16707, 42122, 30345, 49722, 22259, 10828, 41806, 21644, 16915, 40383, 37007, 60191, 7516, 49331, 6308, 41786, 63402, 33919, 45678, 24561, 14898, 63863, 34791, 20743, 17201, 46184, 29783, 17241, 28205, 61312, 6651, 53097, 20824, 25031, 16640, 57491, 8664, 51076, 226, 64164],
[34716, 25703, 61111, 14072, 37973, 18783, 2087, 58487, 42908, 41177, 19139, 38536, 55255, 35267, 40328, 62736, 50662, 12911, 37844, 62460, 6940, 8053, 51868, 13045, 30577, 32525, 61869, 28720, 10473, 44855, 63239, 43436, 19390, 31282, 54449, 64305, 7145, 59049, 6561, 729, 81, 9, 18342],
[16969, 35949, 10042, 6258, 64999, 36721, 60893, 21449, 42748, 5834, 46918, 5287, 50023, 2758, 41255, 7240, 4551, 2562, 44644, 53300, 60117, 57604, 28497, 29219, 53516, 14920, 6844, 32798, 30085, 25836, 8021, 23481, 15638, 52610, 60679, 23143, 27501, 966, 25428, 35138, 53824, 232, 48184],
[52969, 26340, 52551, 11906, 1913, 17454, 32628, 58020, 18570, 55486, 40192, 45463, 14246, 26586, 51952, 55191, 58227, 49236, 47951, 7655, 1874, 48719, 47345, 34706, 8736, 9099, 45779, 44913, 40095, 35842, 59252, 57663, 42617, 23840, 3225, 36105, 23179, 52522, 57000, 49826, 11881, 109, 45041],
[1473, 27380, 31002, 21000, 15544, 18596, 20156, 47151, 37672, 13329, 35931, 37606, 58819, 16923, 31326, 24086, 43319, 55383, 23842, 24813, 50648, 2611, 37410, 31061, 26012, 32536, 20238, 64114, 61288, 48935, 21491, 2825, 28930, 27156, 8641, 22025, 63739, 51648, 6472, 63262, 28900, 170, 49115],
[52370, 53174, 57647, 60279, 57315, 34956, 7646, 12704, 11988, 40284, 25550, 60469, 46145, 53511, 27487, 36276, 40422, 27785, 32554, 14335, 54075, 8127, 36166, 15845, 10144, 41763, 11036, 13468, 1566, 42459, 8061, 60742, 57690, 2562, 52891, 25994, 61961, 44664, 50896, 12205, 30976, 176, 4982],
[28113, 51655, 50728, 7217, 26616, 31868, 16094, 60026, 10687, 2917, 46918, 10574, 3481, 22064, 4710, 35069, 29116, 251, 25426, 26208, 20565, 6392, 2315, 20924, 52158, 58077, 58693, 65478, 10734, 55460, 2738, 35052, 47760, 16231, 63982, 12981, 19886, 53279, 50742, 53545, 13456, 116, 33482],
[58637, 6429, 46183, 57754, 3348, 4631, 64328, 11071, 5898, 37873, 8793, 60963, 13209, 48984, 33460, 4157, 2481, 22165, 37334, 22944, 4723, 35406, 62011, 19983, 19478, 20091, 11171, 20052, 30555, 58296, 38119, 22640, 6260, 20952, 26867, 57971, 24887, 13655, 25602, 29658, 45369, 213, 25450],
[40009, 47332, 42103, 27553, 62643, 32969, 32330, 48600, 17920, 32229, 60915, 48352, 41670, 42065, 6880, 17640, 4077, 46651, 14828, 47163, 58816, 39541, 58325, 50094, 40802, 59653, 41306, 57897, 27659, 13381, 30879, 9444, 63841, 1748, 33440, 38491, 18292, 62141, 46161, 31099, 22201, 149, 18426],
[45080, 61011, 23907, 52998, 9688, 45351, 47228, 5935, 7211, 38322, 57206, 37504, 46815, 57653, 9933, 24668, 63386, 24032, 35758, 1882, 10447, 35043, 8743, 31504, 22354, 39119, 46900, 19715, 59676, 37634, 15778, 18077, 18198, 25103, 42713, 12596, 55852, 51230, 64784, 6859, 361, 19, 31357],
[28140, 5628, 14233, 15954, 42513, 21610, 4322, 53294, 49981, 36211, 33457, 59121, 38039, 46930, 9386, 28092, 58048, 24717, 57373, 24582, 57346, 37684, 46859, 48694, 49061, 36027, 59635, 11927, 54815, 10963, 15300, 3060, 612, 52552, 62940, 12588, 15625, 3125, 625, 125, 25, 5, 38929],
]
times: 1
result:
[
[102, 108, 97, 103, 123, 101, 55, 52, 54, 98, 48, 56, 48, 45, 100, 97, 99, 52, 45, 52, 54, 50, 98, 45, 98, 57, 55, 52, 45, 53, 97, 98, 51, 49, 98, 48, 56, 102, 98, 56, 97, 125],
]
D:\桌面\1>python
Python 2.7.16 (v2.7.16:413a49145e, Mar 4 2019, 01:37:19) [MSC v.1500 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> a = [102, 108, 97, 103, 123, 101, 55, 52, 54, 98, 48, 56, 48, 45, 100, 97, 99, 52, 45, 52, 54, 50, 98, 45, 98, 57, 55, 52, 45, 53, 97, 98, 51, 49, 98, 48, 56, 102, 98, 56, 97, 125]
>>> ''.join(map(chr, a))
'flag{e746b080-dac4-462b-b974-5ab31b08fb8a}'
>>>